ΑΣΕΠ: Οδηγός για τις αριθμητικές ακολουθίες στον 3ο Πανελλήνιο Γραπτό Διαγωνισμό

Ο 3ος Πανελλήνιος Γραπτός Διαγωνισμός του ΑΣΕΠ περιλαμβάνει αριθμητικές ακολουθίες, ένα κρίσιμο μέρος των ερωτημάτων αριθμητικού συλλογισμού που απαιτούν οξεία παρατηρητικότητα και αναλυτική σκέψη. Αυτοί οι γρίφοι δεν είναι απλώς μαθηματικοί, αλλά αποτελούν σημαντικό κριτήριο για την επιτυχή επίδοση των υποψηφίων, δοκιμάζοντας την ικανότητά τους να αποκρυπτογραφούν λογικά μοτίβα.

Η ικανότητα αναγνώρισης και επίλυσης αριθμητικών ακολουθιών αποτελεί θεμελιώδες στοιχείο για την επιτυχία στις εξετάσεις του ΑΣΕΠ, καθώς οι συγκεκριμένοι γρίφοι έχουν καθιερωθεί ως ένα από τα βασικά εργαλεία αξιολόγησης του αριθμητικού συλλογισμού των υποψηφίων.

Αυτή η εξέλιξη έρχεται ως συνέχεια της πάγιας πρακτικής του ΑΣΕΠ να συμπεριλαμβάνει ερωτήματα που δοκιμάζουν την ταχύτητα σκέψης και την κατανόηση βασικών μαθηματικών κανόνων, προετοιμάζοντας τους συμμετέχοντες για τις απαιτήσεις του δημόσιου τομέα.

Τι είναι οι αριθμητικές ακολουθίες και γιατί είναι σημαντικές στις εξετάσεις ΑΣΕΠ

Μια αριθμητική ακολουθία είναι μια σειρά αριθμών που διέπεται από ένα συγκεκριμένο μοτίβο ή κανόνα, όπως μια αριθμητική πρόοδος ή μια γεωμετρική πρόοδος. Τα ερωτήματα αυτού του είδους είναι προσεκτικά σχεδιασμένα για να δοκιμάσουν την ικανότητα των υποψηφίων στην αναγνώριση προτύπων και την εφαρμογή λογικών βημάτων.

Ο εντοπισμός του μοτίβου είναι το πρώτο και πιο κρίσιμο βήμα για την επίλυση οποιασδήποτε ακολουθίας, επιτρέποντας στους εξεταζόμενους να συνεχίσουν τη σειρά ή να βρουν τους αριθμούς που λείπουν.

Παραδείγματα ακολουθιών από προηγούμενους διαγωνισμούς ΑΣΕΠ

Το ΑΣΕΠ έχει παρουσιάσει στο παρελθόν ενδεικτικά παραδείγματα ακολουθιών, τόσο από δια ζώσης όσο και από ηλεκτρονικές εξετάσεις, υπογραμμίζοντας τη σημασία τους. Ας δούμε δύο χαρακτηριστικά παραδείγματα:

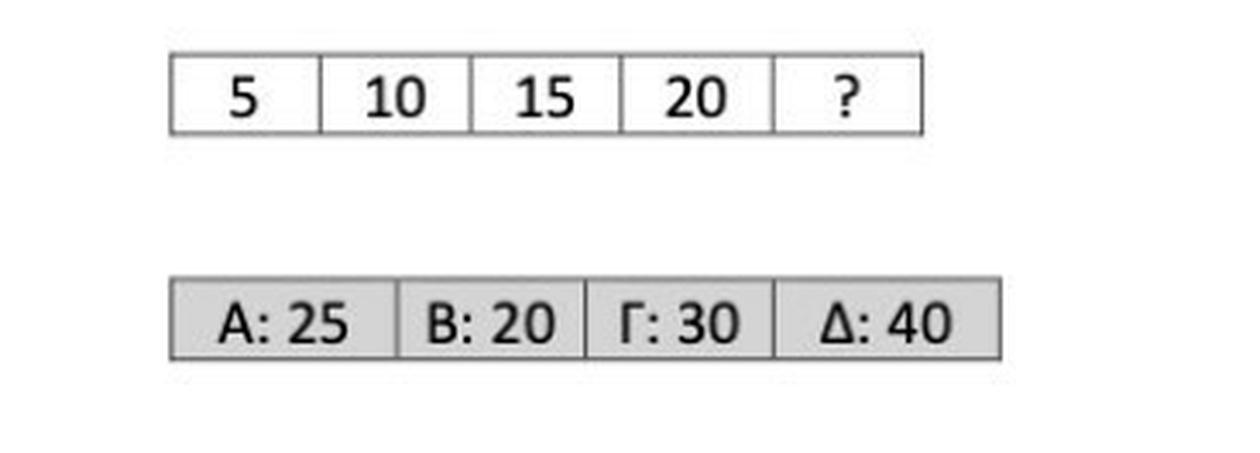
• 1ο παράδειγμα από τον 1ο Γραπτό Πανελλήνιο 2Γ/2022: Μια απλή αριθμητική πρόοδος όπου προστίθεται σταθερά ο αριθμός 5. Η ακολουθία 5, 10, 15, 20, 25 βασίζεται στην προσθήκη του 5 σε κάθε προηγούμενο όρο (5+5=10, 10+5=15 κ.ο.κ.).
• 2ο παράδειγμα από τον 1Γ/2024 (ΤΕ Δασοπονίας): Εδώ, η ακολουθία 10, 20, 25, 50, 55, ? απαιτεί την αναγνώριση ενός μικτού μοτίβου. Η σωστή απάντηση είναι το 110. Η λογική είναι: 10 Χ 2 = 20, 20 + 5 = 25, 25 Χ 2 = 50, 50 + 5 = 55, 55 Χ 2 = 110.

Οι αριθμητικές ακολουθίες αποτελούν ένα σημαντικό δείκτη αναλυτικής ικανότητας και γρήγορης σκέψης, στοιχεία που είναι απαραίτητα για την επιτυχή σταδιοδρομία στον δημόσιο τομέα. Νομικοί κύκλοι και εκπαιδευτικοί αναλυτές επισημαίνουν ότι η συστηματική εξάσκηση σε τέτοιου είδους ερωτήματα μπορεί να αυξήσει σημαντικά τις πιθανότητες επιτυχίας, καθώς ακονίζει το μυαλό και ενισχύει την ικανότητα επίλυσης προβλημάτων υπό πίεση χρόνου.

Βασικές μέθοδοι επίλυσης αριθμητικών ακολουθιών

Για την αποτελεσματική επίλυση των αριθμητικών ακολουθιών, είναι σημαντικό να γνωρίζετε τις βασικές κατηγορίες και μεθόδους:

Αριθμητική πρόοδος

Στην αριθμητική πρόοδο, ο επόμενος όρος προκύπτει προσθέτοντας μια σταθερή διαφορά στον προηγούμενο. Για παράδειγμα, στην ακολουθία 3, 6, 9, 12, 15, το μοτίβο είναι η προσθήκη του 3 (κοινή διαφορά), άρα ο επόμενος αριθμός είναι το 18.

Γεωμετρική πρόοδος

Αντίθετα, στη γεωμετρική πρόοδο, ο επόμενος όρος προκύπτει πολλαπλασιάζοντας με έναν σταθερό λόγο. Στην ακολουθία 2, 6, 18, 54, 162, ο κοινός λόγος είναι το 3, οδηγώντας στον επόμενο αριθμό 486.

Μικτές ακολουθίες και σύνθετες μέθοδοι

Οι μικτές ακολουθίες είναι ιδιαίτερα σημαντικές, καθώς συχνά εμφανίζονται σε απαιτητικές εξετάσεις. Μπορεί να περιλαμβάνουν συνδυασμό πράξεων (πρόσθεση, αφαίρεση, πολλαπλασιασμός, διαίρεση) ή συνδυασμό αριθμητικών και γεωμετρικών προόδων. Για την αποκωδικοποίησή τους, βοηθά η μέθοδος των διαφορών ή διπλών διαφορων, που επιτρέπει την αναγνώριση του υποκείμενου μοτίβου.

Ένα παράδειγμα είναι η ακολουθία 25, 47, 91, 179, ?, όπου οι διαφορές διπλασιάζονται κάθε φορά (22, 44, 88), οδηγώντας στο 355 (179 + 176).

Τέσσερις βασικοί τρόποι για την επίλυση αριθμητικών ακολουθιών είναι:

1. Η παρατήρηση των διαφορών μεταξύ διαδοχικών όρων.
2. Η μέθοδος της σταθερής διαίρεσης για εντοπισμό γεωμετρικής προόδου.
3. Η παραγοντοποίηση των όρων σε γινόμενο δύο παραγόντων για κρυφά μοτίβα.
4. Η εξέταση αν η σειρά σχετίζεται με τετράγωνα ή κύβους αριθμών, ειδικά όταν οι διαφορές αυξάνονται απότομα.

Δοκιμάστε τις γνώσεις σας: 10 ερωτήματα ΑΣΕΠ

Σύμφωνα με τον ΑΣΕΠ, αυτά τα είδη ερωτημάτων αφορούν στην αναγνώριση των σχέσεων αριθμών που εμφανίζονται σε μία σειρά. Σε κάθε ερώτηση πρέπει να βρίσκετε ποιος αριθμός συμπληρώνει ορθά τη σειρά και αντικαθιστά το ερωτηματικό (?). Εσείς πρέπει να εντοπίσετε τη σωστή απάντηση από τις πέντε (5) εναλλακτικές απαντήσεις που θα σας δίνονται. Δοκιμάστε τις δυνάμεις σας στα ακόλουθα δέκα (10) ερωτήματα ακολουθιών:

1. Ποιος αριθμός αντικαθιστά το ερωτηματικό στην ακολουθία;
Επεξήγηση: 11 Χ 12 = 132, 12 Χ 13 = 156, 13 Χ 14 = 182, 14 Χ 15 = 210, 16 Χ 17 = 272.

2. Ποιος αριθμός αντικαθιστά το ερωτηματικό στην ακολουθία;
Επεξήγηση: 186, 186 + 24 = 210, 210 + 48 = 258, 258 + 24 = 282, 282 + 48 = 330, 330 + 24 = 354.

3. Ποιος αριθμός αντικαθιστά το ερωτηματικό στην ακολουθία;
Επεξήγηση: 11, 11 + 42 = 53, 53 + 40 = 93, 93 + 36 = 129, 129 + 30 = 159, 159 + 22 = 181.

4. Ποιος αριθμός αντικαθιστά το ερωτηματικό στην ακολουθία;
Επεξήγηση: 3, 3 Χ 4 – 3 = 9, 9 Χ 4 – 3 = 33, 33 Χ 4 – 3 = 129, 129 Χ 4 – 3 = 513, 513 Χ 4 – 3 = 2049.

5. Ποιος αριθμός αντικαθιστά το ερωτηματικό στην ακολουθία;
Επεξήγηση: 383, 383 + (8+3) = 394, 394 + (9+4) = 407, 407 + (0+7) = 414, 414 + (1+4) = 419, 419 + (1+9) = 429.

6. Ποιος αριθμός αντικαθιστά το ερωτηματικό στην ακολουθία;
Επεξήγηση: 4, 4 Χ 6 – 6 = 18, 18 Χ 5 – 5 = 85, 85 Χ 4 – 4 = 336, 336 Χ 3 – 3 = 1005, 1005 Χ 2 – 2 = 2008.

7. Ποιος αριθμός αντικαθιστά το ερωτηματικό στην ακολουθία;
Επεξήγηση: 9, 9 + 256 = 265, 265 + 128 = 393, 393 + 64 = 457, 457 + 32 = 489, 489 + 16 = 505.

8. Ποιος αριθμός αντικαθιστά το ερωτηματικό στην ακολουθία;
Επεξήγηση: 7, 7+2 Χ 5 = 17, 17+3 Χ 6 = 35, 35+4 Χ 7 = 63, 63+5 Χ 8 = 103, 103+6 Χ 9 = 157.

9. Ποιος αριθμός αντικαθιστά το ερωτηματικό στην ακολουθία;
Επεξήγηση: 52 Χ 1 – 1 = 24, 62 Χ 2 – 2 = 70, 72 Χ 3 – 3 = 144, 82 Χ 4 – 4 = 252, 92 Χ 5 – 5 = 400, 102 Χ 6 – 6 = 594.

10. Ποιος αριθμός αντικαθιστά το ερωτηματικό στην ακολουθία;
Επεξήγηση: 2048, 2048 : 4 + 4 = 516, 516 Χ 2 = 1032, 1032 : 4 + 4 = 262, 262 Χ 2 = 524, 524 : 4 + 4 = 135, 135 Χ 2 = 270.

Προετοιμασία για την επιτυχία στις εξετάσεις ΑΣΕΠ

Η συστηματική εξάσκηση σε αριθμητικές ακολουθίες είναι απαραίτητη για την επιτυχία στον 3ο Πανελλήνιο Γραπτό Διαγωνισμό του ΑΣΕΠ. Η κατανόηση των διαφορετικών τύπων μοτίβων και η εφαρμογή των κατάλληλων μεθόδων επίλυσης θα ενισχύσει σημαντικά την αναλυτική σας σκέψη και την ικανότητά σας να διαχειρίζεστε αποτελεσματικά τον χρόνο.

Με την κατάλληλη προετοιμασία, οι υποψήφιοι μπορούν να αντιμετωπίσουν με αυτοπεποίθηση αυτά τα απαιτητικά ερωτήματα και να αυξήσουν τις πιθανότητες να επιτύχουν τον στόχο τους.